Rendimiento de Optimización en Embeddings Sintéticos Gaussianos y de Árbol

Tabla de Enlaces

Resumen y 1. Introducción

1. Trabajos Relacionados

2. Técnicas de Relajación Convexa para SVMs Hiperbólicos

   3.1 Preliminares

   3.2 Formulación Original del HSVM

   3.3 Formulación Semidefinida

   3.4 Relajación Momento-Suma-de-Cuadrados

3. Experimentos

   4.1 Conjunto de Datos Sintético

   4.2 Conjunto de Datos Real

4. Discusiones, Agradecimientos y Referencias

   \

A. Demostraciones

B. Extracción de Soluciones en Formulación Relajada

C. Sobre la Jerarquía de Relajación Momento Suma-de-Cuadrados

D. Escalado de Platt [31]

E. Resultados Experimentales Detallados

F. Máquina de Vectores de Soporte Hiperbólica Robusta

4.1 Conjunto de Datos Sintético

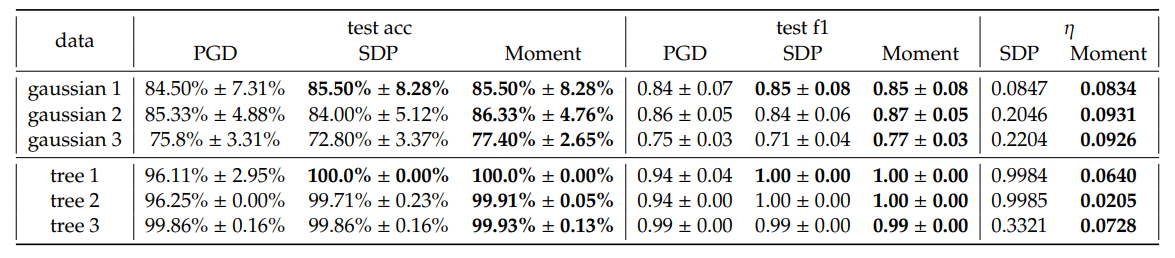
\ En general, observamos una pequeña mejora en la precisión promedio de las pruebas y en el puntaje F1 ponderado de SDP y Moment en relación con PGD. Notablemente, observamos que Moment a menudo muestra mejoras más consistentes en comparación con SDP, en la mayoría de las configuraciones. Además, Moment proporciona brechas de optimalidad 𝜂 más pequeñas que SDP. Esto coincide con nuestra expectativa de que Moment es más ajustado que el SDP.

\ Aunque en algunos casos, por ejemplo cuando 𝐾 = 5, Moment logra pérdidas significativamente menores en comparación con PGD y SDP, generalmente no es el caso. Enfatizamos que estas pérdidas no son mediciones directas de la generalizabilidad de los separadores hiperbólicos de margen máximo; más bien, son combinaciones de maximización de margen y penalización por clasificación errónea que escala con 𝐶. Por lo tanto, la observación de que el rendimiento en precisión de prueba y puntaje F1 ponderado es mejor, aunque la pérdida calculada utilizando soluciones extraídas de SDP y Moment es a veces mayor que la de PGD, podría deberse al complicado paisaje de pérdida. Más específicamente, los aumentos observados en la pérdida pueden atribuirse a las complejidades del paisaje en lugar de a la efectividad de los métodos de optimización. Basándose en los resultados de precisión y puntaje F1, empíricamente los métodos SDP y Moment identifican soluciones que generalizan mejor que aquellas obtenidas ejecutando solo descenso de gradiante. Proporcionamos un análisis más detallado sobre el efecto de los hiperparámetros en el Apéndice E.2 y el tiempo de ejecución en la Tabla 4. El límite de decisión para Gaussiano 1 se visualiza en la Figura 5.

\

\ Incrustación de Árbol Sintético. Como los espacios hiperbólicos son buenos para incrustar árboles, generamos grafos de árbol aleatorios y los incrustamos en H2 siguiendo a Mishne et al. [6]. Específicamente, etiquetamos los nodos como positivos si son hijos de un nodo especificado y negativos en caso contrario. Nuestros modelos se evalúan luego para la clasificación de subárboles, con el objetivo de identificar un límite que incluya todos los nodos hijos dentro del mismo subárbol. Esta tarea tiene varias aplicaciones prácticas. Por ejemplo, si el árbol representa un conjunto de tokens, el límite de decisión puede resaltar regiones semánticas en el espacio hiperbólico que corresponden a los subárboles del grafo de datos. Enfatizamos que una característica común en dicha tarea de clasificación de subárboles es el desequilibrio de datos, que generalmente conduce a una pobre generalizabilidad. Por lo tanto, nuestro objetivo es utilizar esta tarea para evaluar el rendimiento de nuestros métodos bajo esta configuración desafiante. Se seleccionan tres incrustaciones y se visualizan en la Figura 3 y el rendimiento se resume en la Tabla 1. El tiempo de ejecución de los árboles seleccionados se puede encontrar en la Tabla 4. El límite de decisión del árbol 2 se visualiza en la Figura 6.

\ Similar a los resultados de los conjuntos de datos gaussianos sintéticos, observamos un mejor rendimiento de SDP y Moment en comparación con PGD, y debido al desequilibrio de datos con el que los métodos GD típicamente tienen dificultades, tenemos una mayor ganancia en el puntaje F1 ponderado en este caso. Además, observamos grandes brechas de optimalidad para SDP pero una brecha muy ajustada para Moment, certificando la optimalidad de Moment incluso cuando el desequilibrio de clases es severo.

\

\

:::info Autores:

(1) Sheng Yang, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (shengyang@g.harvard.edu);

(2) Peihan Liu, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (peihanliu@fas.harvard.edu);

(3) Cengiz Pehlevan, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, Center for Brain Science, Harvard University, Cambridge, MA, y Kempner Institute for the Study of Natural and Artificial Intelligence, Harvard University, Cambridge, MA (cpehlevan@seas.harvard.edu).

:::

:::info Este artículo está disponible en arxiv bajo licencia CC by-SA 4.0 Deed (Attribution-Sharealike 4.0 International).

:::

\